2020 LGS Matematik Sorularının Çözümleri20 Haziran

20 Haziran 2020 tiarihinde yapılan LGS Matematik sorularının çözümlerini sizler için hazırladık. LGS’ye hazırlanan öğrenciler soruların çözümlerini inceleyebilirler. İşte 2020 LGS Matematik çözümleri…

2020 LGS Matematik Çözümleri

Soru 1

a, b birer doğal sayı olmak üzere a√b=√a²b dir.
Bir bilye atma oyununa ait, kısa kenar uzunluğu 1 m olan dokuz eş dikdörtgensel bölgeden oluşan oyun parkuru aşağıda verilmiştir.

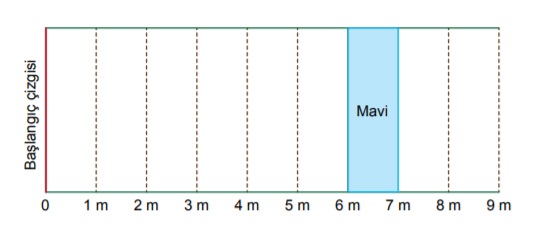
Başlangıç çizgisinden atış yapan bir oyuncunun attığı bilye, parkurda gösterilen mavi bölgede kalmıştır.
Buna göre bu bilyenin başlangıç çizgisine uzaklığı metre cinsinden aşağıdakilerden hangisi olamaz?

Çözüm: Soruda bilyenin mavi bölgede durduğu söylenmiştir. Mavi bölge 6m ile 7m arasında denk gelmektedir. Soruda bizden bilyenin başlangıçtaki noktaya uzaklığı hangisi olamaz diye soruyor.
a şıkkına baktığımızda;
2√10 = √2².10 = √40 olduğuna göre bu sayı 6 dan büyük 7 den küçük bir sayıdır.
b şıkkına baktığımızda;
3√5 = √3².5 = √45 olduğuna göre bu sayı 6 dan büyük 7 den küçük bir sayıdır.
c şıkkına baktığımızda;
4√3 = √4².3 = √48 olduğuna göre bu sayı 6 dan büyük 7 den küçük bir sayıdır.
d şıkkına baktığımızda;
2√13 = √2².13 = √52 olduğuna göre bu sayı 7 dan büyük 8 den küçük bir sayıdır.
CEVAP: D Şıkkı

Soru 2

Ayşe’nin bir yılda okuduğu kitapların türlerine göre dağılımı aşağıdaki daire grafiği ile gösterilmiştir.
Grafik: Ayşe’nin Okuduğu Kitapların Türlerinin Dağılımı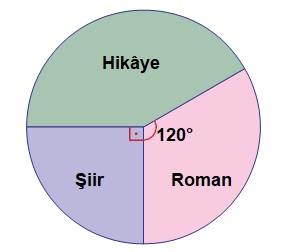

Kareli zeminde verilen sütun grafiklerinden hangisi yukarıdaki daire grafiğine uygun oluşturulmuştur?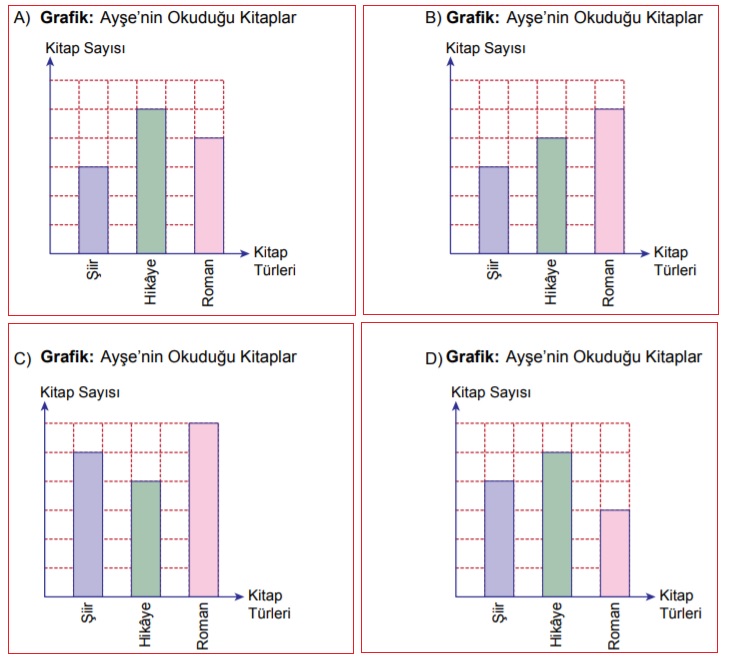

Çözüm: Soruda pasta grafiğinde Roman kitapları 120 iken Şiir kitapları 90 ve Hikaye kitapları 150 olarak bulunur.
120, 90 ve 150 sayıları ortak bölenlere bölündüğünde(sadeleştirildiğinde)
4, 3 ve 5 olarak bulunur.
Şiir 3
Hikaye 5
Roman 4
Sütun grafiğinde buna uygun olan seçenek A şıkkında verilmiştir.

CEVAP: A Şıkkı

Soru 3

Bir ondalık gösterimin, basamak değerleri toplamı şeklinde yazılmasına ondalık gösterimin çözümlenmesi denir.
Bir basketbol takımındaki beş oyuncunun boy uzunluklarının çözümlenmiş şekli aşağıdaki tabloda verilmiştir.
Tablo: Oyuncuların Boylarının Uzunlukları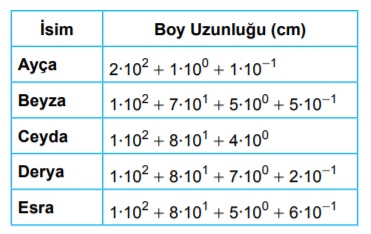

Takımın antrenörü, boyu 185 santimetreden kısa olan oyunculardan birini oyun kurucu olarak oynatacaktır.
Buna göre verilen oyuncular arasında oyun kurucu olarak oynayabilecek kaç oyuncu vardır?

Çözüm:
Ayça’nın boyu
2.10² + 1.10⁰ + 1.10-¹ =2.100 + 1.1+1.0,1
= 200+1+0,1
=201,1 cm
Beyza’nın boyu
1.10² + 7.10¹+ 5.10⁰ + 5.10-¹ =1.100+7.10+5.1+5.0,1
=100+70+5+0,5
=175,5 cm
Ceyda’nın boyu
1.10² + 8.10¹+ 4.10⁰ =1.100+8.10+4.1
=100+80+4
=184 cm
Derya’nın boyu
1.10² + 8.10¹+ 7.10⁰ + 2.10-¹=1.100+8.10+7.1+2.0,1
=100+80+7+0,2
=187,2 cm
Esra’nın boyu
1.10² + 8.10¹+ 5.10⁰ + 6.10-¹=1.100+8.10+5.1+6.0,1
=100+80+5+0,6
=185,6 cm

185 ten kısa olan yalnızca Beyza ve Ceyda olduğuna göre
CEVAP: C Şıkkı

Soru 4

a, b, c birer doğal sayı olmak üzere,
a√b=√a²b dir.
a+√b+c+√b=(a+c)√b dir.
Bir şehrin demir yolu hatları üzerindeki istasyonlar aşağıdaki şekilde noktalar ile gösterilmiştir. Aynı hat üzerinde bulunan ardışık iki istasyon arasındaki mesafeler birbirine eşittir.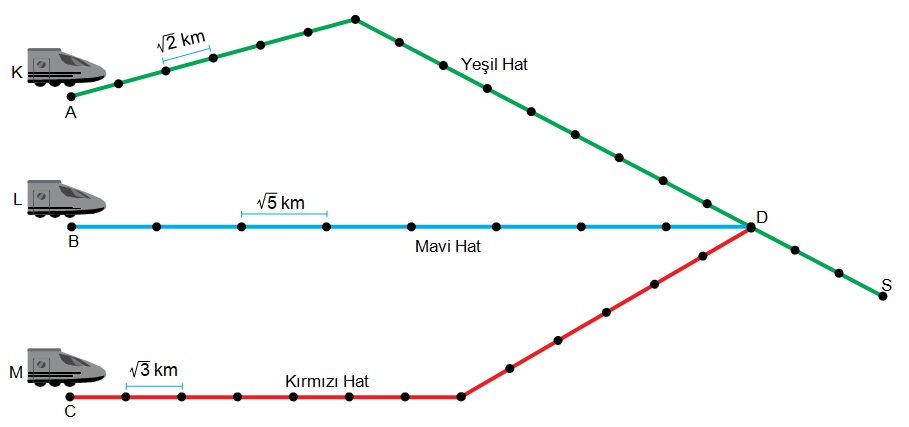

A, B, C istasyonlarından hareket eden K, L ve M trenleri ortak olan D istasyonundan sonra yeşil hattı kullanarak S istasyonuna ulaşıyorlar.
Bu trenlerin gittikleri yolların uzunluğuna göre doğru sıralanışı aşağıdakilerden hangisidir?

Çözüm:
K treni yeşil hattı kullanıyor ve D istasyonuna kadar toplam 15 birim ilerliyor. Her bir birim √2 olduğuna göre
K= 15√2
L treni önce Mavi hat üzerinde D istasyonuna kadar 8 birim ilerliyor her bir birim √5 olduğuna göre 8√5
L= 8√5
M treni kırmızı hat üzerinde D istasyonuna kadar 13 birim ilerliyor
M= 13√3
M>K>L
CEVAP: D Şıkkı

Soru 5

Kenarlarının uzunlukları x metre ve 2x metre olan dikdörtgen şeklindeki oyun parkının planı Şekil I’de verilmiştir. Bu oyun parkının kenarları 2’şer metre uzatılarak Şekil II’deki gibi dikdörtgen biçiminde bir oyun parkı planlanmıştır.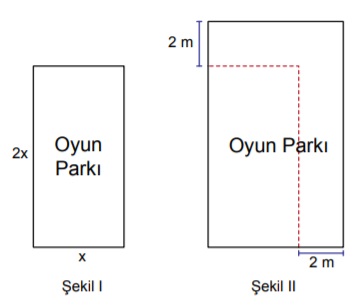


Buna göre Şekil II’deki oyun parkının alanının Şekil I’deki oyun parkının alanından kaç metrekare fazla olduğunu veren cebirsel ifade aşağıdakilerden hangisidir?

Çözüm:
Şekil I’deki oyun parkının alanı
2x.x = 2x²
Şekil II’deki oyun parkının alanı
(2x+2).(x+2) = 2x² + 4x+ 2x + 4 = 2x² + 6x + 4
Farkı bulalım;
2x² + 6x + 4 – 2x² = 6x+4
CEVAP: A Şıkkı

Soru 6

Yükseklikleri santimetre cinsinden birer tam sayı olan aşağıdaki dikdörtgenler prizması şeklindeki kutuların her birinden üçer adet vardır.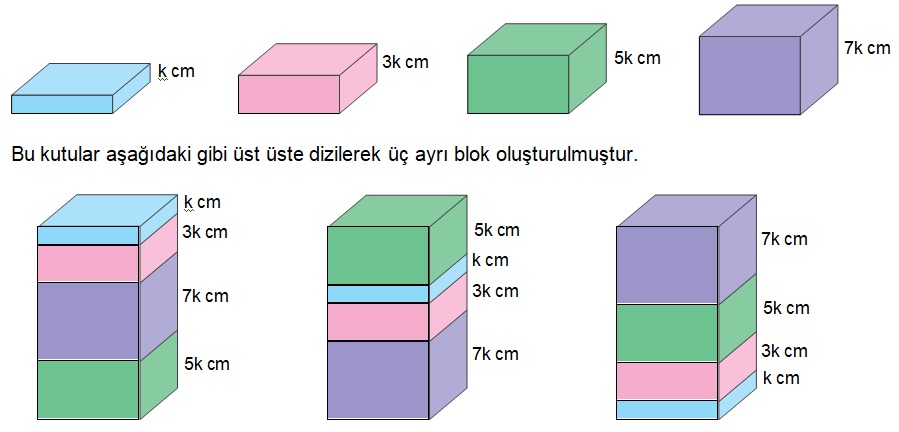


Bloklardaki kutuların yerleri değiştirilmeden bu üç blok üst üste konularak bir kule oluşturuluyor. Daha sonra kulenin en üstünde bulunan kutu alınıyor.
Son durumda bu kulenin yüksekliğinin santimetre cinsinden değeri aşağıdakilerden hangisi olamaz?

Çözüm:
1. kule 16 k
2. kule 16 k
3. kule 16 k
üç kule üst üste konulduğunda 48 k yapıyor fakat en üstteki kutu çıkarılıyor.
1. seçenek 1. kuledeki çıkarılırsa 48-1 = 47 k
2. seçenek 2. kuledeki çıkarılırsa 48-5 = 43 k
3. seçenek 3. kuledeki çıkarılırsa 48-7 = 41 k
Bu durumda kulenin boyu 47, 43 ve 41 ‘in katları olmalı.
Şıklarda
A şıkkında 94 47’nin katı
C şıkkında 86 43’ün katı
D şıkkında 82 41’in katı olduğu için
Cevap 90 olacak.

CEVAP: B Şıkkı

Soru 7

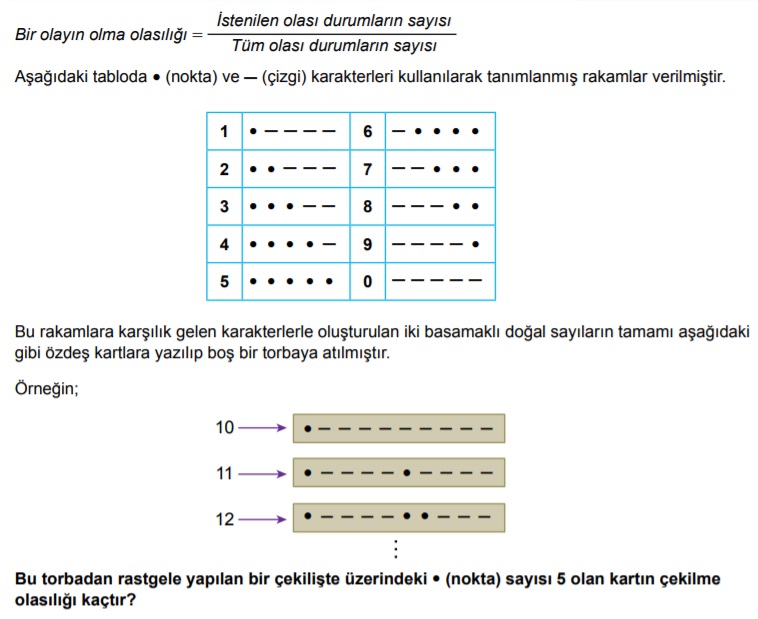
Bu torbadan rastgele yapılan bir çekilişte üzerindeki • (nokta) sayısı 5 olan kartın çekilme olasılığı kaçtır?

Çözüm:
2 basamaklı 90 sayı vardır.
Bu sayılardan üzerinde 5 nokta içeren sayılar
14 (1 kartı üzerinde 1 nokta 4 kartı üzerinde 4 nokta)
16
23
27
32
38
41
49
50
61
69
72
78
83
86
94
96
sayılarıdır.
Olasılık = 17/90

CEVAP: C Şıkkı

Soru 8

Aşağıda her birinin kütlesi 3 g olan sarı boncuklardan ve her birinin kütlesi 5 g olan mavi boncuklardan yeterli sayıda verilmiştir. Bu boncuklar kullanılarak bir kolye yapılmıştır.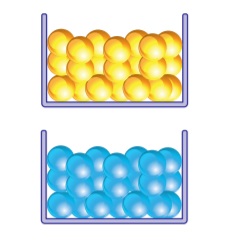

Kolyedeki mavi boncukların toplam kütlesi sarı boncukların toplam kütlesine eşittir.
Kullanılan boncukların toplam kütlesi 230 gramdan az olduğuna göre bu kolyedeki sarı boncukların sayısı ile mavi boncukların sayısı arasındaki fark en fazla kaçtır?

Çözüm:
Mavi Boncuk toplam ağırlığı = Sarı Boncuk toplam ağırlığı
1 sarı boncuk ağırlığı 3 gr
1 mavi boncuk ağırlığı 5 gr
3 ile 5 in ebob u 15 dir. 3 ile 5 i kullanarak eşit ağırlıkta boncuk oluşturmak için 15in katında bir sayı kullanmalıyız. Ama toplamları da 230 dan küçük olmalı.
Toplam Ağırlık < 230
15 in 7 katı 105 yapar ve bu ağırlık sarı topların toplam ağırlığı olsun
105 gram da mavi topların toplam ağırlığı olacaktır. Toplam ağırlık 220 yapar.
Sarı boncukların sayısı 105/3 = 35
Mavi boncukların sayısı 105/5= 21
Topların farkı 35-21 = 14 bulunur.

CEVAP: A Şıkkı

Soru 9

Aşağıda dört farklı renkteki kartların her birinden üçer adet verilmiştir. Aynı renkteki kartların üzerinde aynı kareköklü ifade yazmaktadır.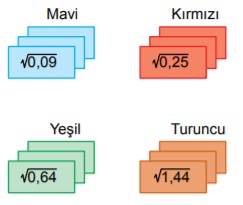

Eymen, bu kartlardan seçerek üstlerinde yazan kareköklü ifadeleri topladığında bir doğal sayı elde etmektedir.
Buna göre Eymen en fazla kaç kart seçmiştir?

Çözüm:
Sayıları karakök dışarısına çıkardığımızda
0,3
0,5
0,8
1,2
oluyor.
Bu sayıları topladığımızda doğal sayı olması için (en fazla kaç olur dediğine göre en küçük olanlardan başlayarak)
0,3×3
0,5×3
0,8×3
1,2×1
Toplam 6 sayısı elde edilir. 10 kart kullandığımız için cevap 10 olacak.
CEVAP: C Şıkkı

Soru 10

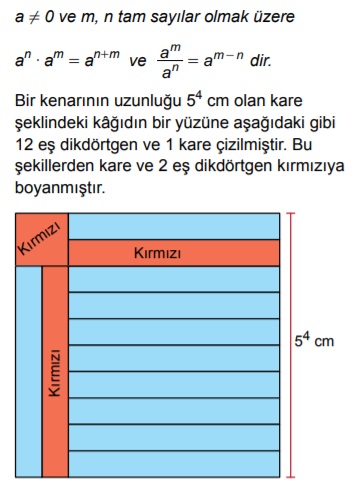
Buna göre kırmızı bölgelerin alanları toplamı kaç santimetrekaredir?

Çözüm:
Şekli biraz değiştirirsek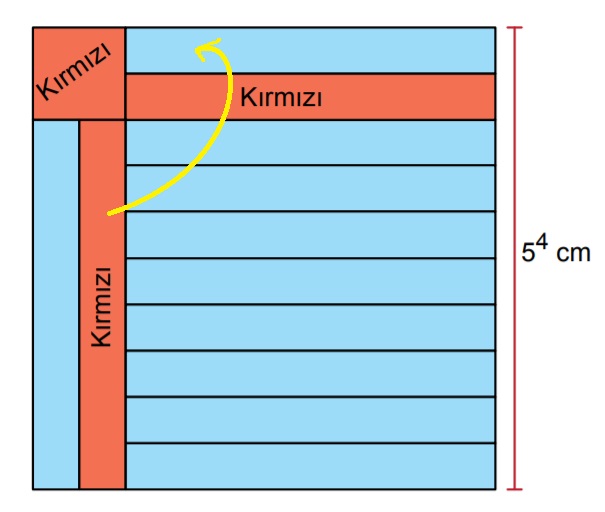


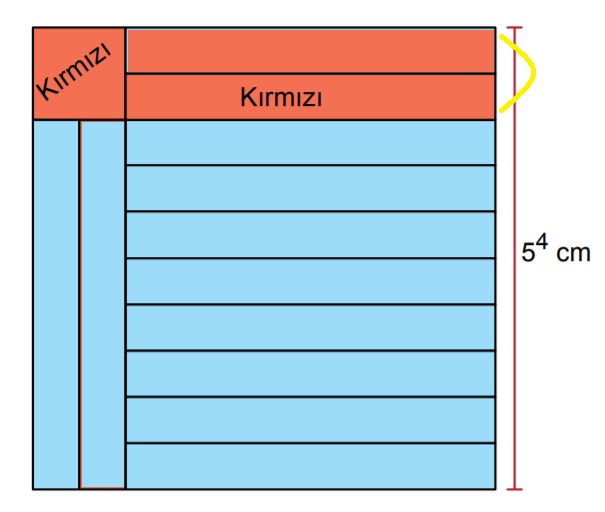
şekilde gördüğünüz gibi istenilen alan toplam alanın 5 te biri olacaktır.
Toplam Alan= (5⁴)² olarak yazılır ve 5⁸ bulunur.
Kırmızı Alan=5⁸/5 ifadesi de 5⁸/5¹ yazılır ve 5⁸-¹ = 5⁷ bulunur.
CEVAP: B Şıkkı

Soru 11

Dikdörtgen şeklindeki bir kâğıt, alanları santimetrekare cinsinden 10’dan büyük birer tam kare pozitif tam sayıya eşit olan karesel bölgelere aşağıdaki gibi ayrılmıştır.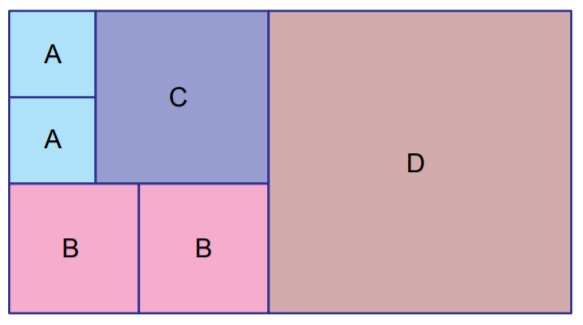

Eşit alanlı bölgeler aynı harf ile gösterildiğine göre dikdörtgen şeklindeki bu kâğıdın bir yüzünün alanı en az kaç santimetrekaredir?

Çözüm:
10 dan büyük en küçük tam kare pozitif tam sayı 16 dır. Bu nedenle
A harfinin alanı 16 olsun. Bir kenarı 4 cm olur.
C harfi olan alanın bir kenarı 8 cm olur.
B harfi olan alanın bir kenarı 6 olmak zorunda.
D ise A ve B nin kenarlarına göre hesaplanır ve 14 cm olur.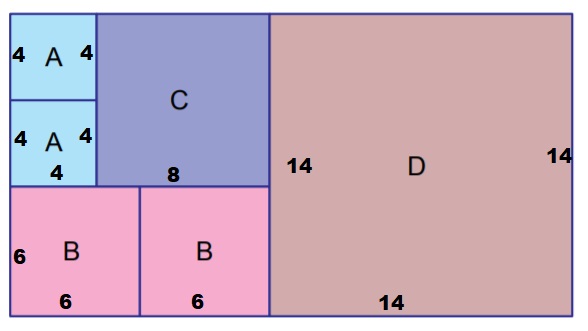

Yeni şeklin kısa kenar uzunluğu 14 cm, uzun kenarı ise 26 cm olur.
Alan=14×26 = 364

CEVAP: C Şıkkı

Soru 12

Alanı 1050 cm² olan kare şeklindeki bir panoya kenarlarından birinin uzunluğu 5’in tam sayı kuvveti, diğerinin uzunluğu 2’nin tam sayı kuvveti olan dikdörtgen şeklindeki bir afiş, pano yüzeyinden taşmayacak şekilde asılacaktır.
Buna göre afişin bir yüzünün alanı en fazla kaç santimetrekaredir?

Çözüm:
1050 cm² olan karenin bir kenar uzunluğu 32 cm olarak alınabilir. Bu kare panoya
5 in tam sayı kuvveti olan en büyük 25
2 nin tam sayı kuvveti olan en büyük 32 olarak alınır.
Alan= 25×32 = 800 cm²

CEVAP: B Şıkkı

Soru 13

Bir lokantada hazırlanan yemek çeşitleri ve porsiyon sayıları sütun grafiği ile bu yemekler için kullanılan toplam 60 g tuzun yemek çeşitlerine göre dağılımı daire grafiği ile aşağıda gösterilmiştir. Bir çeşit yemeğin her porsiyonunda eşit miktarda tuz bulunmaktadır.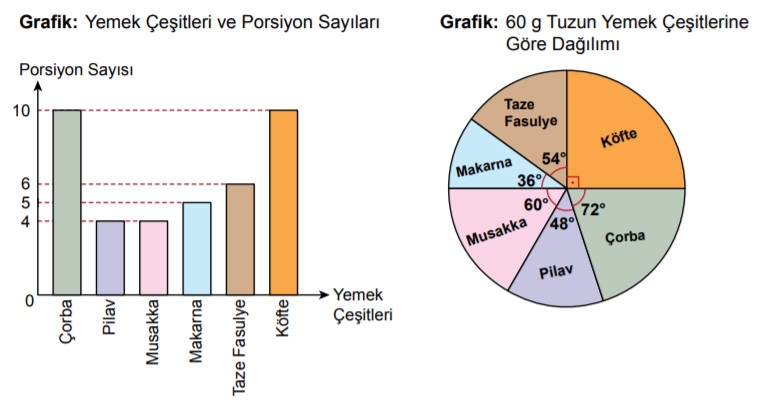

Bu lokantada üç farklı yemekten birer porsiyon yiyen bir müşteri toplam 5 g tuz tüketmiştir.
Buna göre bu müşterinin yediği yemekler aşağıdakilerden hangisidir?

Çözüm:
60 gram tuzun önce yemeklere dağılımına bakalım.
360 derecelik grafikte
Köfte 90 derece ve 90*60/360=15 g (10 porsiyonda 15 g ise 1 porsiyonda 1,5 g tuz)
Çorba 72 derece 72*60/360= 12 g (10 porsiyonda 12 g ise 1 porsiyonda 1,2 g tuz)
Pilav 48 derece ve 48*60/360= 8 g (4 porsiyonda 8 g ise 1 porsiyonda 2 g tuz)
Musakka 60 derece ve 60*60/360 10 g (4 porsiyonda 10 g ise 1 porsiyonda 2,5 g tuz)
Makarna 36 derece 36*60/360=6 g (5 porsiyonda 6 g ise 1 porsiyonda 1,2 g tuz)
Taze Fasulye 54 derece 54*60/360=9 g (6 porsiyonda 9 g ise 1 porsiyonda 1,5 g tuz)
Bu durumda toplamı 5 gram yapan yemekler
Köfte + Pilav + Taze Fasulye

CEVAP: D Şıkkı

Soru 14

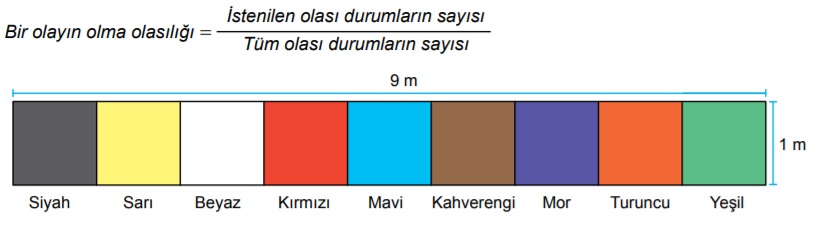
Kenarlarının uzunlukları 1 m ve 9 m olan dikdörtgen biçimindeki bir halının ön yüzü, şekildeki gibi farklı renklere boyanmıştır. Bu renklerin her birinin kapladığı karesel bölgenin alanı birbirine eşittir.
Bu halı, parçalarda aynı renk olmayacak şekilde iki parçaya bölünecektir.
Buna göre bu parçalardan birinin boyalı yüzünün alanının, diğerinin boyalı yüzünün alanının 2 katı olması olasılığı kaçtır?

Çözüm:
İkiye bölündüğünde bir parçanın alanı diğer parçanın alanının 2 katıl olması durumları
3 kare bir parçada, 6 kare bir parçada olabilir.
6 kare bir parçada,3 kare bir parçada olabilir. Yani 2 durum söz konusu.
Toplam ikiye bölme durumu ise 8 dir. 8 farklı şekilde bölünebilir.
Şimdi olasılığa bakalım.
2/8 = 1/4

CEVAP: B Şıkkı

Soru 15

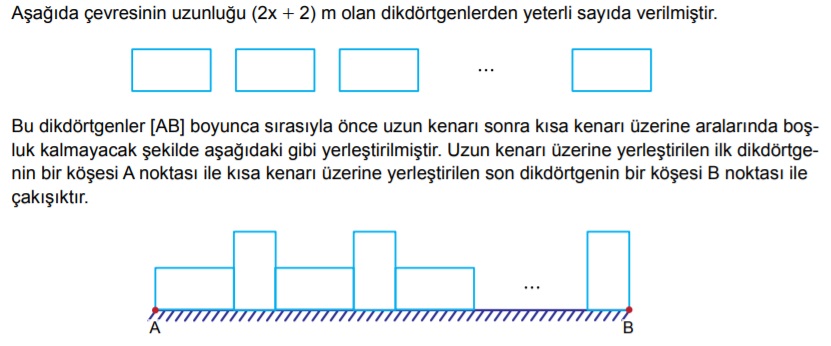
Bu dikdörtgenler (x + 1) kez kısa kenarı üzerine yerleştirildiğine göre [AB]’nın uzunluğunu metre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?

Çözüm:
Dikdörtgenin çevresi 2x+2 verilmiş.
Şekilde A ile B arasına yerleştirilen bir uzun bir kısa kenarın uzunluğu x+1 eder. Soruda kısa kenar x+1 kez yerleştirildiğine göre diyor. Yani A-B arası uzunluk
(x+1).(x+1) olarak bulunur
Bu cebirsel ifade
x² +2x+1 olarak yazılabilir.

CEVAP: D Şıkkı

Soru 16

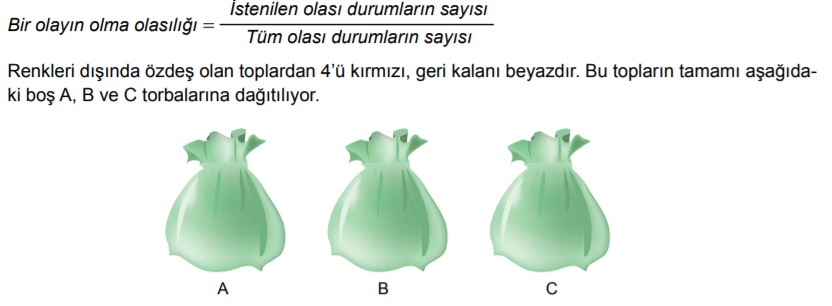
Bu torbaların her birinden rastgele çekilen bir topun kırmızı olma olasılığı birbirine eşittir.
Buna göre başlangıçtaki beyaz top sayısı aşağıdakilerden hangisi olamaz?

Çözüm:
Kırmızı top 4 adet olduğuna göre 3 torbaya
birinci torbaya 1 ikinci torbaya 1 ve üçüncü torbaya 2 şeklinde yerleştirilmiş olmalı.
Torbalardan kırmızı çıkma olasılığı eşit olduğuna göre
1. torbadaki ve 2. torbadaki beyaz top sayısı eşit olmalı 3. torbadaki beyaz top sayısı ise 2 katı olmalı. Yani 1. torbada x sayısında beyaz top varsa 2. torbada x beyaz top ve 3. torbada 2x beyaz top vardır.
Toplam 4x beyaz top vardır.
Şıklarda 4 ün katı olmayan yani 4 e bölünemeyen tek seçenek B şıkkındaki 82 dir.
CEVAP: B Şıkkı

Soru 17

Her birinin kütlesi 40 kg’dan az ve birbirine eşit olan buğday çuvalları aşağıdaki gibi bir kantarda tartıldığında çuvalların toplam kütlesi 720 kg gelmektedir.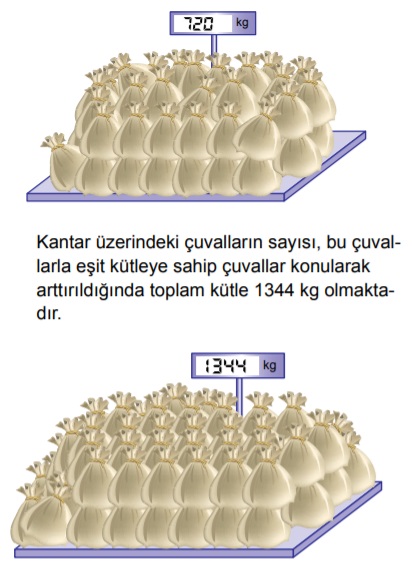


Buna göre kantar üzerine sonradan konulan çuvalların sayısı en az kaçtır?

Çözüm:
1344 kg ile 720 kg un EKOK’unu bulalım
48 bulunur. Fakat 40 kilodan az olduğu için 24 olarak alınır.
Yani torbaların ağırlığı 24 bulunur.
1344-720=624 kg sonradan konulan ağırlık
624/24=26 adet torba vardır.

CEVAP: C Şıkkı

Soru 18

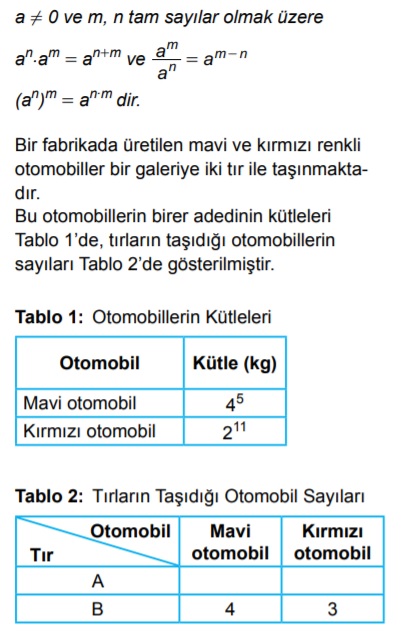
A tırı ile taşınan mavi ve kırmızı otomobillerin sayıları birbirine eşittir.
İki tırın taşıdığı otomobillerin toplam kütlesi 2¹⁴ kg olduğuna göre A tırı ile taşınan otomobil sayısı kaçtır?

Çözüm:
B tırı 4×4⁵ + 3×2¹² = 2x2x2¹⁰+3×2¹² = 2×2¹¹+3×2¹¹ = 5×2¹¹
Toplam 2¹⁴ olduğuna göre
A tırı = 2¹⁴ – 5×2¹¹ = 2x2x2x2¹¹ -5×2¹¹ yazılır buradan 3×2¹¹ bulunur.
A tırında 3×2¹¹ olması için
Mavi otomobil 2 Kırmızı 2 seçilmeli
2×2¹⁰ + 2×2¹¹ = 2¹¹ + 2×2¹¹=3×2¹¹ bulunur. Yani toplam 4 otomobil vardır.
CEVAP: B Şıkkı

Soru 19

Kare şeklindeki boş bir panoya kare şeklindeki üç eş mavi karton, köşegenleri panonun köşegeni ile çakışacak şekilde aşağıdaki gibi yerleştirilmiştir.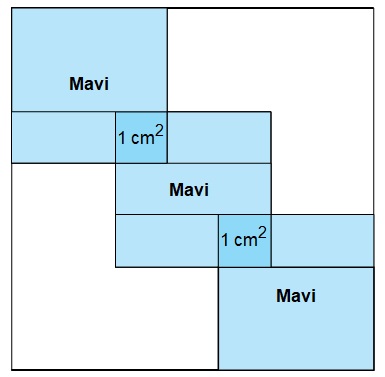

Panoda boş bırakılan bölgelerin alanları toplamı 6x² + 36x + 54 santimetrekaredir. Kartonların üst üste gelen bölgelerinin her biri, alanları 1 cm2 olan karesel bölgelerdir.
Buna göre panonun çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?

Çözüm:
6x² + 36x + 54 ifadesini 6 ortak çarpanda yazarsak
6.(x+3)² olarak yazılabilir.
Şekli düzenlersek,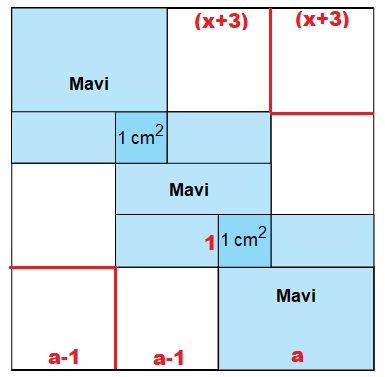

Beyaz bölge toplam 6 kare parça olacaktır.
Beyaz bölgenin alanı 6.(x+3)² olduğuna göre her bir beyaz karenin kenarı (x+3) olarak bulunur.
a-1=x+3 denkleminden
a=x+4 bulunur.
Bir kenar uzunluğu a-1+a-1+a olduğuna göre a yerine x+4 yazalım
3x+10 bulunur.
Karenin Çevresi
4.(3x+10) = 12x+40 bulunur.
CEVAP: A Şıkkı

Soru 20

Bir okulun Ordu iline düzenleyeceği gezide ziyaret edilecek yerlerle ilgili yapılan anket çalışmasında her bir öğrenci ziyaret edilebilecek yerlerle ilgili yalnız bir tercihte bulunmuştur. Bu anketin sonuçları sütun grafiği ile ankete katılan kız ve erkek öğrencilerin sayılarının dağılımı daire grafiği ile aşağıda gösterilmiştir.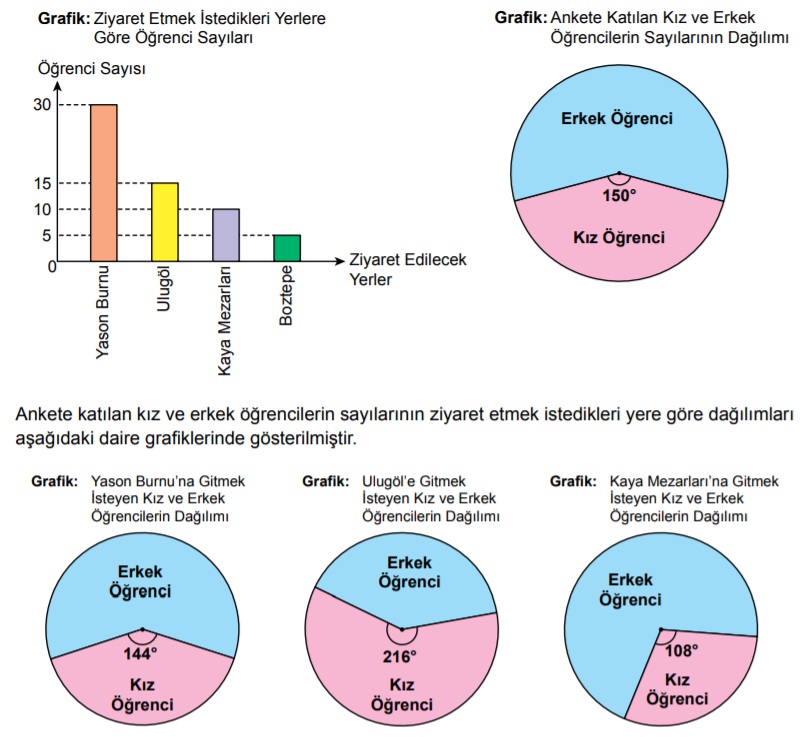

Yukarıda verilenlere göre Boztepe’yi ziyaret etmek isteyen erkek öğrencilerin sayısı kaçtır?

Çözüm:
Yason burnu 30 öğrenci 30*144/360=12 kız, 18 Erkek
Ulugöl 15 öğrenci 15*216/360= 9 kız, 6 Erkek
Kaya Mezarları 10 Öğrenci 10*108/360= 3 kız, 7 Erkek
Kız Öğrenci = 24 + Boztepe seçen kız
Erkek Öğrenci = 31 + Boztepe seçen erkek
Boztepe seçen kız + Boztepe seçen erkek = 5 öğrenci

Kız öğrencilerle Erkek öğrencilerin oranı
Kız/Erkek=150/210 = 5/7
olması için
Boztepe seçen kız sayısı 1
Boztepe seçen erken sayısı 4 olarak bulunur.

CEVAP: D Şıkkı